Fluid Mechanics and Hydraulic Machines Very Important Questions
Fluid Mechanics And Hydraulic Machines is a very important topic of Engineering comes under the Mechanical and Civil streams.This section will provide you with the Important questions which are asked in exams under the Fluid Mechanics and Hydraulic Machines with the combination of all objective type questions, subjective type questions and a section with numerical problems.

Hydraulic machine
What is a fluid?
Three common states of matter are solid, liquid, and gas.
What is mechanics?
The dictionary says mechanics is the application of the laws of force and motion.There are two branches, statics and dynamics.
So, putting it all together, fluid mechanics is the application of the laws of force and motion to fluids i.e. liquids and gases.
Questions with their Answers on Fluid Mechanics And Hydraulic Machines
1. A fluid is a substance that
(a) Always expands until it fills any container
(b) Has the same shear stress at a point
regardless of its motion
(c) Cannot remain at rest under action of any
shear force
(d) Cannot be subjected to shear forces
ANSWER: (b)
2. Length of mercury column at a place at analtitude will vary with respect to that at ground in a
(a) Linear relation
(b) hyperbolic relation
(c) Parabolic relation.
(d) Manner first slowly and then steeply
ANSWER: (d)
3. When power is transmitted through a considerable distance by means of water under
pressure, the maximum power is transmitted when frictional loss of head is
(a) One third of the total head supplied
(b) Half of the total head supplied
(c) 10% of the total head
(d) 17.7% 0f the total head.
ANSWER: (a)
4. A rotameter is a device used to measure
(a) Velocity of fluid in pipes
(b) Velocity of gauges
(c) Votex flow
(d) Flow of fluids
ANSWER: (d)
5. The continuity equation
(a) Expresses relationship between hydraulic
parameters of flow
(b) Expresses the relationship, between work and
energy
(c) Is based on Bernoulli’s theorem
(d) Relates the mass rate of flow along a stream
line.
ANSWER: (d)
6. Of the following, dimensionless parameter is
(a) Pressure coefficient
(b) Froude number
(c) Darcy Weisbach friction factor
(d) All of the above
ANSWER: (d)
7. One dimensional flow
(a) Restricted to flow in a straight line
(b) Neglects changes in a transverse direction
(c) Steady uniform flow
(d) A uniform flow
ANSWER: (b)
8. Steady flow occurs when
(a) Pressure does not change along the flow
(b) Velocity does not change
(c) Conditions change gradually with time
(d) Conditions do not change with time at any point.
ANSWER: (d)
9. Equation Continuity of fluids is applicable only when the flow is
(a) Steady
(b) One dimensional
(c) Compressive
(d) All of the above
ANSWER: (d)
10. If the particles of a fluid attain such velocities that vary from point to point in magnitude and
direction as well as from instant, the flow is
(a) Uniform flow
(b) Steady flow
(c) Turbulent flow
(d) Laminar flow
ANSWER: (c)
Short Type Questions On Fluid Mechanics & Hydraulic Machines
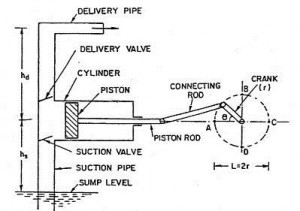
1. Why the Centrifugal Pump is called High Discharge pump?
Centrifugal Pump
Ans. Centrifugal pump is a kinetic device. The centrifugal pump uses the centrifugal force to push out the fluid. So the liquid entering the pump receives kinetic energy from the rotating impeller. The centrifugal action of the impeller accelerates the liquid to a high velocity, transferring
mechanical (rotational) energy to the liquid. So it discharges the liquid in high rate. It is given in the following formulae:
Centrifugal force F= (M*V2)/R.
Where,
M-Mass
V-Velocity
R-Radius
2. How Cavitation can be eliminated by Pump?
Ans. Cavitation means bubbles are forming in the liquid.To avoid Cavitation, we have to increase the Pump size to One or Two Inch;To increase the pressure of the Suction Head, or Decrease the Pump Speed.
3. Why Cavitation will occur in Centrifugal Pump and not in Displacement Pump?
Ans. The formation of cavities (or bubbles) is induced by flow separation, or non-uniform flow velocities, inside a pump casing. In centrifugal pumps the eye of the pump impeller is smaller than the flow area of pipe. This decrease in flow area of pump results in increase in flow rate. So pressure drop happened between pump suction and the vanes of the impeller. Here air bubbles or cavities are formed because of liquid vapour due to increase in temperature in impeller. This air bubbles are transmitted to pump which forms cavitation.
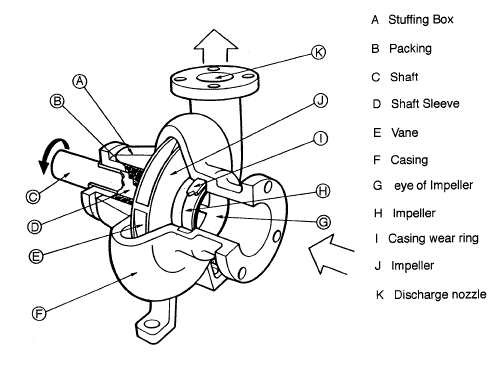
4. Which Pump is more Efficient Centrifugal Pump or Reciprocating Pump?
Ans. Centrifugal pump. Because flow rate is higher compared to reciprocating pump. Flow is smooth and it requires less space to install. Lower initial cost and lower maintenance cost.
Centrifugal Pump
5. Why Centrifugal Pump is not called as a Positive Displacement Type of Pump?
Ans. The centrifugal has varying flow depending on pressure or head, whereas the Positive Displacement pump has more or less constant flow regardless of pressure.
Likewise viscosity is constant for positive displacement pump where centrifugal pump have up and down value because the higher viscosity liquids fill the clearances of the pump causing a higher volumetric efficiency. When there is a viscosity change in supply there is also greater loss in the system. This means change in pump flow affected by the pressure change.
One more example is, positive displacement pump has more or less constant efficiency, where centrifugal pump has varying efficiency rate
Long Type Questions On Fluid Mechanics & Hydraulic Machines
Problem 1
Consider a fluid (of density ρ) in incompressible, laminar flow in a plane narrow slit of length L and width W formed by two flat parallel walls that are a distance 2B apart. End effects may be neglected because B << W << L. The fluid flows under the influence of both a pressure difference Δp and gravity.
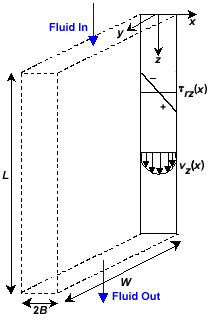
Fig 1
Figure.
Fluid flow in plane narrow slit.a) Using a differential shell momentum balance, determine expressions for the steady-state shear stress distribution and the velocity profile for a Newtonian fluid (of viscosity μ).
b) Obtain expressions for the maximum velocity, average velocity and the mass flow rate for slit flow.
(a) For a plane narrow slit, the natural choice is rectangular Cartesian coordinates. Since the fluid flow is in the z-direction, vx = 0,vy = 0, and only vz exists. Further, vz is independent of z and it is meaningful to postulate that velocity vz = vz(x) and pressure p= p(z). The only nonvanishing components of the stress tensor are τxz = τzx, which depend only on x.
Consider now a thin rectangular slab (shell) perpendicular to the x-direction extending a distance W in the y-direction and a distance L in the z-direction. A ‘rate of z-momentum’ balance over this thin shell of thickness Δx in the fluid is of the form:
Rate of z-momentum In − Out + Generation = AccumulationAt steady-state, the accumulation term is zero. Momentum can go ‘in’ and ‘out’ of the shell by both the convective and molecular mechanisms. Since vz(x) is the same at both ends of the slit, the convective terms cancel out because (ρ vz vz WΔx)|z = 0 = (ρ vz vz W Δx)|z = L. Only the molecular term (L W τxz ) remains to be considered. Generation of z-momentum occurs by the pressure force (p W Δx) and gravity force (ρ g W L Δx). On substituting these contributions into the z-momentum balance, we get
(L W τxz ) | x − (L W τxz ) | x+Δx+ ( p 0 − p L ) W Δx + ρ g W L Δx = 0
Dividing the above equation by L W Δx yields
( τxz | x+Δx- τxz | x ) / Δx = ( p 0 − p L + ρ g L) /L (2)
On taking the limit as Δx → 0, the left-hand side of the above equation is the definition of the derivative. The right-hand side may be compactly and conveniently written by introducing the modified pressure P, which is the sum of the pressure and gravitational terms. The general definition of the modified pressure is P = p + ρ g h , where h is the distance upward (in the direction opposed to gravity) from a reference plane of choice. Since the z-axis points downward in this problem, h = − z and therefore P = p − ρ g z . Thus, P0 = p0 at z = 0 and PL = pL − ρ g L at z = L giving p0 − pL + ρ g L = P0 − PL ≡ ΔP. Thus, equation (2) gives
(dτxz ) /dx=( ΔP)/L (3)
Equation (3) on integration leads to the following expression for the shear stress distribution:
τxz = X(ΔP)/L+ C1 (4)
The constant of integration C1 is determined later using boundary conditions.
It is worth noting that equations (3) and (4) apply to both Newtonian and non-Newtonian fluids, and provide starting points for many fluid flow problems in rectangular Cartesian coordinates.
Substituting Newton’s law of viscosity for τxz in equation (4) gives
− μ(dvz)/dx =x(ΔP)/L+ C1 (5)
The above first-order differential equation is simply integrated to obtain the following velocity profile: vz =x2(ΔP)/2 μ L–x( C1)/ μ+ C2 (6)
The no-slip boundary conditions at the two fixed walls are BC 1: at x = B, vz = 0 (7)
BC 2: at x = −B, vz = 0 (8)
Using these, the integration constants may be evaluated as C1 = 0 and C2 = ΔP B2 / (2 μ L). On substituting C1 = 0 in equation (4), the final expression for the shear stress (or momentum flux) distribution is found to be linear as given by
τxz =x( ΔP)/L (9)
Further, substitution of the integration constants into equation (6) gives the final expression for the velocity profile as
vz= (ΔP B 2)/( 2 μ L)(1-((x)/B)2 ) (10)
It is observed that the velocity distribution for laminar, incompressible flow of a Newtonian fluid in a plane narrow slit is parabolic.
b) From the velocity profile, various useful quantities may be derived.
(i) The maximum velocity occurs at x = 0 (where dvz/dx = 0). Therefore,
vz,max= vz, | x = 0 =( ΔP B2)/ 2 μ L (11)
(ii) The average velocity is obtained by dividing the volumetric flow rate by the cross-sectional area as shown below.
vz,avg = ( − B∫ B vz W dx)/( B∫ B W dx )=(1/2B) -B∫ B vz dx=( ΔP B2)/( 3 μ L)=2/3 vz,max (12)
Thus, the ratio of the average velocity to the maximum velocity for Newtonian fluid flow in a narrow slit is 2/3.
(iii) The mass rate of flow is obtained by integrating the velocity profile over the cross section of the slit as follows.
W= B∫ B ρ vz W dx = ρ W (2 B) vz,avg (13)
Thus, the mass flow rate is the product of the density ρ, the cross-sectional area (2 B W) and the average velocity vz,avg. On substituting vz,avg from equation (12), the final expression for the mass rate of flow is
w =(2 ΔP B3 W ρ)/ 3 μ L (14)
The flow rate vs. pressure drop (w vs. ΔP) expression above is the slit analog of the Hagen-Poiseuille equation (originally for circular tubes). It is a result worth noting because it provides the starting point for creeping flow in many systems (e.g., radial flow between two parallel circular disks; and flow between two stationary concentric spheres).
Finally, it may be noted that the above analysis is valid when B << W. If the slit thickness B is of the same order of magnitude as the slit width W, then vz = vz (x, y), i.e., vz is not a function of only x. If W = 2B, then a solution can be obtained for flow in a square duct.
PROBLEM 2
Consider a Newtonian liquid (of viscosity μ and density ρ) in laminar flow down an inclined flat plate of length L and width W. The liquid flows as a falling film with negligible rippling under the influence of gravity. End effects may be neglected because Land W are large compared to the film thickness δ.
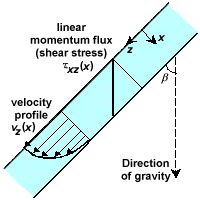
Fig 2
Figure. Newtonian liquid flow in a falling film.a) Determine the steady-state velocity distribution.
b) Obtain the mass rate of flow and average velocity in the falling film.
c) What is the force exerted by the liquid on the plate in the flow direction?
d) Derive the velocity distribution and average velocity for the case where x is replaced by a coordinate x‘ measured away from the plate (i.e., x‘ = 0 at the plate and x‘ = δ at the liquid-gas interface).
Ans (a)
For axial flow in rectangular Cartesian coordinates, the differential equation for the momentum flux is
(dτxz)/( dx)=( ΔP)/(L) (1)
where P is a modified pressure, which is the sum of both the pressure and gravity terms, that is, ΔP = Δp + ρ g L cos β. Here,β is the angle of inclination of the z-axis with the vertical. Since the flow is solely under the influence of gravity, Δp = 0 and therefore ΔP/L = ρ g cos β. On integration,
τxz = ρ g x cos β + C1 (2)
On using the boundary condition at the liquid-gas interface (τxz = 0 at x = 0), the constant of integration C1 is found to be zero. This gives the expression for the shear stress τxz for laminar flow in a falling film as
τxz = ρ g x cos β (3)
It must be noted that the above momentum flux expression holds for both Newtonian and non-Newtonian fluids (and does not depend on the type of fluid).
The shear stress for a Newtonian fluid (as per Newton’s law of viscosity) is given by
(τxz)/( dx)=- μdvz (4)
To obtain the velocity distribution, there are two possible approaches.
In the first approach, equations (3) and (4) are combined to eliminate τxz and get a first-order differential equation for the velocity as given below.
(dvz)(dx)=-(( ρ g cos β)/( μ ))(x) (5)
On integrating, vz = − ρ g x2 cos β/(2μ) + C2. On using the no-slip boundary condition at the solid surface (vz = 0 at x = δ ), C2= ρ g δ2 cos β/(2μ). Thus, the final expression for the velocity distribution is parabolic as given below.








0 comments:
Post a Comment